Read almost any book on survival, and there will be a number of methods described for finding direction using the sun.
As with many things that are written in books, there are many "borrowed" ideas. One person writes something, another copies it, but changes it in a subtle manner, it gets copied again etc. Pretty soon, a lot of the important data is lost, or has been morphed into something that is no longer accurate. Try searching the Internet for information on finding direction using the sun. It would appear that there are some simple methods to determine "exactly" the direction of N-S / E-W.

According to "most" information that is "out there," some of the favorite methods of finding direction include the Shadow Stick and the Watch Method.

I decided to try out these methods to see how will they work. I also experimented with finding Longitude.

The data for the following photographs was collected on July 19, 2005. (Location: N43° 27' W79° 51') The sun changes its angle in the sky on a daily basis so the information presented here is one "snap shot." At some later point in time, I may just sit down to do the math to predict exactly how well these methods work for any day of the year. For now, I will provide measured information so that the reader might get a better "gut feel" for how these methods work.

This was the setup that I used.

A piece of cardboard with a bamboo skewer inserted.

Every 5 - 10 minutes, I would mark the shadow position.

A closer view of the plotted points.

(The other lines on the chart were drawn in for measuring angles.)

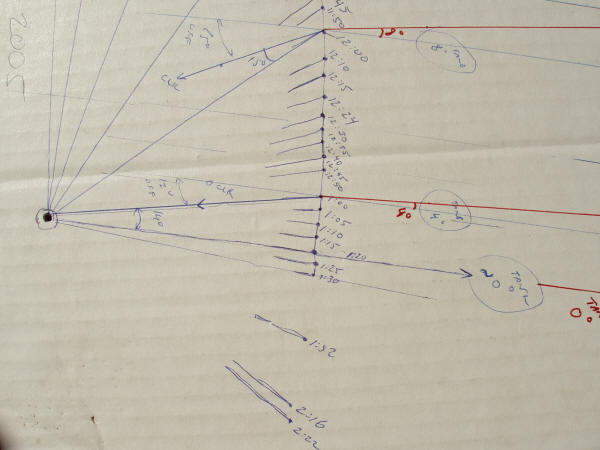A closer view, showing the plotted points.

Note: the times written on the chart were using DST.

Tangent/Perpendicular Method

A "classic" method to find direction is to plot two shadow points and then draw a line between them. This is claimed to be an E-W line, and the perpendicular would then be the N-S line.

Since the sun's shadow moves in an arc (on most of the planet), clearly this method has some error.

Many of the descriptions of this method imply that the resultant direction is "absolute."

Here is a close-up.

The pointers (sticks) show what is claimed to be the cardinal points.

The compass (adjusted for declination) shows the true N-S direction. Clearly there is error here!

Time (EST)	Error from True North (Degrees)
7:00	23
8:00	20
9:00	17
10:00	15
11:00	8
12:00	4
12:20	0

This table shows the approximate amount of error based on the method described above.

In the morning, we have the greatest error, and it gets smaller as we approach the solar noon.

Note that the error was only 0 at 12:20 - more on that later when we discuss longitude.

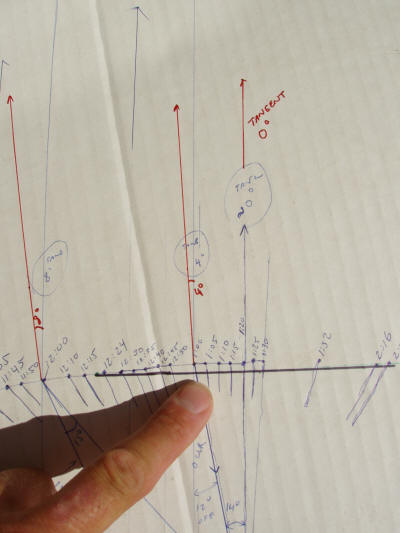A more exact method is to plot two points at equidistant times on both sides of "noon."

In this photo, the black line shows such a line.

The points plotted were on either side of "solar noon."

Have a look at the discussion below about longitude for an explanation of the difference between "clock" noon, and solar noon.

This black line pointed exactly W-E, and the perpendicular line, N-S.

Since the path of the sun is symmetrical around solar noon, this method will always give true north.

The methodology is to plot a shadow point, then wait until the shadow is shortest, then plot another point an equal amount of time later.

Watch Method

Another method of finding direction is the "watch" method. The procedure is to point the hour hand of a watch towards the sun. A line that passes mid-way between the hour hand and the "12" mark on the watch is supposed to point south. The bamboo pointer shows where south should be by this method.

The picture shows the same set-up, only this time using a normal analog watch. Again the bamboo pointer shows where south should be.

The compass points to true north/south.

Look at the angle between the pointer and the compass.

Clearly there is error in this method.

A close-up of the error.

Almost all of the references that I have seen for this method make one think that it is exact.

Time (EST)	Error from True North (Degrees)
7:00	35
8:00	30
9:00	30
10:00	30
11:00	25
12:00	12
12:20	0

How much error is there in this method?

The adjacent table shows what I got on that day. There is certainly some experimental error in my results, but one gets the point. This is far from being an exact method.

Not only does this method have a large error, it also requires a watch.

Longitude and some Theory

There is a lot of background in how our earth moves, and the systems that we use to find out where we are, or direction of travel. I will give a brief introduction.

(Please put the words "more or less" in front of just about everything that I am writing! I am trying to describe the general principles - not the exact science.)

Our earth rotates on it axis every 24 hours. (Think about the more or less!)
We have defined there to be 360 degrees in a circle.
So, the earth rotates 360/24 or 15 degrees every hour.

Longitude is our system for determining how many degrees we are from Greenwich England (zero degrees.)
At noon in Greenwich, the sun will be directly overhead.
One hour later, it will be directly overhead a point that is 15 degrees West of Greenwich.
If we were to give the longitude of this point, we would say it is 15 degrees west - (kind of makes sense doesn't it!?)

From this, we can see that time and degrees of longitude are directly related.

Now a subtlety. It is "common" knowledge that the sun is overhead (ie, at its highest point) at noon. But let's think about that one a bit.
Each time-zone is 15 degrees "wide" - or takes up 15 degrees of longitude. So, a person who sees the sun directly overhead (ie, at its highest point) at one "edge" of the time-zone means that someone at the other "edge" of the time-zone will be seeing the sun 15 degrees off from overhead. So the actual statement, is that the sun is overhead within one hour of noon. How far off is determined by how far to the East or West we are within one time zone - or expressed another way, it is determined by our longitude.

If we record the exact time that the sun is directly overhead, we can do a bit of math and figure out our longitude. How cool is that?

This is an enlargement of the shadow plot.

Notice the line that was drawn at 1:20. This was the shadow that was cast that pointed exactly to true north.

If one doesn't have a compass, it is also the "shortest" shadow.

Let's do the math:

First, we need to work in standard time.
The sun was directly overhead at 1:20 pm DST.
Converting to EST we get 12:20pm.
Since this was done in the Eastern Standard Time Zone, we "know" that we are 5 time zones from Greenwich.
Each time zone is 15 degrees, so our longitude is 5*15 = 75 degrees W plus a "bit."

How big is this bit? Well, solar noon (when the sun was actually at its highest point in the sky) was at 20 minutes past the hour.
20 minutes is one third of an hour - so we must be one third of 15 degrees further West.
(20/60) * 15 = 5 degrees

So my longitude was 75 + 5 = 80 degrees West.

I took out my GPS and measured my actual longitude to be 79 degrees, 51 minutes.

The error in my shadow plot resulted in an error of only 9 minutes.
If we were to plot this difference on a map, then my estimate of position was off by 6.7 nautical miles, or 12.3 kms!
Pretty good for a stick, a piece of paper and a watch!

(By the way, a nautical mile is equal to the distance formed by one minute of longitude at the equator.)

For more exact results with alternate methods, do some reading on sextants.

Conclusions and Notes

The data presented here represents one set of numbers on one day of the year. The errors will change with latitude and time of the year.

The watch/clock method, while sounding very cool and exact is one of the worst methods to use. Check the various available references - almost all imply this method to be perfect, or very close!

The tangent/perpendicular method is pretty good in the summer when the sun is quite high in the sky. Towards winter, the sun will be lower and the shadow will have more of a curve to it. Think about whether this would make this method more or less accurate.

Finding the solar noon sun - or shortest shadow - will give an exact result, as will drawing a line between two points that are plotted at times that are the same amount before and after noon.

As for longitude - the real key is to have an accurate watch. Given that these cost about a dollar these days, who needs an expensive GPS to find longitude!

--Rob

Survival Navigation

READ THE DISCLAIMER